Evin çatısı ile çadırın neredeyse aynı şekilde olmasına dikkat ediyor musunuz? Tekrar bakarsanız, her iki ucunda 2 üçgenden oluşuyormuş gibi görünüyor, daha sonra dikdörtgen bir örtüyle örtülüyor. Bu şekil aynı zamanda üçgen prizma olarak da bilinir. Bu denir çünkü taban ve kapak üçgen şeklindedir. Geometride, üçgen prizmaların tanımını ve formülünü inceleyeceğiz. Bu vesileyle, bu materyali daha iyi anlayabilmek için sorunun çeşitli örneklerini de tartışacağız.
Bir prizma, bir kapak ve aynı n-kenarlı şekle sahip bir tabanı olan bir şekildir, dikey kenarlar ise dikdörtgen şeklindedir.
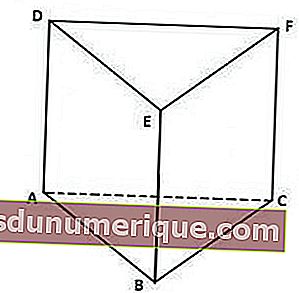
Üçgen prizmalar aşağıdaki özelliklere sahiptir:
Uyumlu üçgen bir tabana ve kapağa sahiptir.
Yukarıdaki resimden, prizmanın kapağı, yani DEF üçgeni, tabanı olarak ABC üçgeni ile aynı şekil ve boyuta sahiptir.
Dikey kenar olarak dikdörtgen.
Gördüğünüz gibi, yukarıdaki prizma, dikeyin her iki yanında ACFD, BCFE ve ABED dikdörtgenleri ile sınırlı üç dikdörtgen ile sınırlıdır.
5 kenar, 9 kenar ve 6 köşeye sahiptir.
Üçgen prizmanın 5 kenarı, tabanın 1 tarafı, kapağın 1 tarafı ve 3 kenardan oluşur. 9 nervür 3 dik, 3 tabanın 3 kenarı ve 3 kapağın yanından oluşur. Ayrıca, 6 köşe noktası A, B, C, D, E ve F noktalarıdır.
Şimdi, üçgen prizmanın özelliklerini ve anlamını bildiğimize göre, üçgen prizma formüllerini ve problemlerinin örneklerini tanımanın zamanı geldi.
Üçgen Prizma Formülleri ve Örnek Problemler
Öğrendiğimiz 2 çeşit üçgen prizma formülü olacaktır. Hacmi bulmak için formül ve yüzey alanını bulmak için formül. Formüller şu şekildedir:
Ses
Hacim için aşağıdaki formülü kullanacağız:
V = taban alanı × yükseklik
veya
V = (½ x a x h) × prizmanın yüksekliği
Öyleyse, bunu daha iyi anlamak için, bu sorunun bir örneğine bakalım:
Bir prizma 10 cm yüksekliğindedir. Prizmanın tabanı, yan uzunlukları sırasıyla 4 cm ve 3 cm olan dik üçgen şeklindedir. Bu üçgen prizmanın hacmi nedir?
Çözüm:
Burada, bilinen sayıları aşağıdaki gibi bir formüle koymamız gerekiyor:
V = (½ x a x h) × prizmanın yüksekliği
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Yüzey alanı
Üçgen prizmanın yüzey alanını hesaplarken aşağıdaki gibi bir formül kullanacağız:
L = (tabanın 2 x alanı) + (tüm dikey kenarların alanı)
üçgen eşkenar ise şu formülü kullanabilirsiniz:
L = (tabanın 2 x alanı) + (düşeyin bir tarafının 3 x alanı)
Veya formül olabilir:
L = (2 x taban alanı) + (tabanın çevresi x prizma yüksekliği)
Bu formülün nasıl uygulandığını görmek için bu sorunun bir örneğine bakalım. İşte sorunun bir örneği:
12 cm yüksekliğinde, 5 cm kenar uzunluğunda ve 8 cm yüksekliğinde eşkenar üçgen prizma vardır. O halde bu üçgen prizmanın yüzey alanı nedir?
Çözüm:
Yüzey alanını bulmak için, aşağıdaki gibi üçgen prizmanın yüzey alanı formülünü kullanıyoruz:
L = (tabanın 2 x alanı) + (bir dikey düzlemin 3 x alanı)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
İşte bilmeniz gereken çeşitli üçgen prizma formülleri ve bazı problem örnekleri bunlar. Hâlâ kafanız karıştıysa, yorumlar sütununda sorabilir veya dünyanın güvenilir çevrimiçi eğitim platformu olan Smart Class'ı deneyebilirsiniz.









