Bir otoyolda iki araç arasında bir çarpışmaya hiç tanık oldunuz mu? İki araç çarpıştığında ne olur? Fizikten bakıldığında, bir çarpışmanın ölümcül olup olmadığı aracın momentumuna göre belirlenir. Bunu daha iyi anlamak için, momentum ve itme ile ilgili materyali inceleyelim.
Fizikte momentum, hareketli bir nesnenin sahip olduğu miktar olarak tanımlanır. Momentum miktarı, nesnenin kütlesine ve hızına bağlı olacaktır. Matematiksel olarak, momentum p = mv olarak yazılabilir, burada p momentumdur (kg m / s), m nesnenin kütlesi (kg) ve v nesnenin hızıdır (m / s).
Bu formüle dayanarak, momentumun nesnenin hızıyla orantılı olduğu görülebilir. Dolayısıyla, momentumun yönü hızının yönü ile aynıdır, ayrıca bir nesnenin hızı arttıkça momentumu da artar.
Bu arada dürtü, ortalama kuvvetin ve kuvvetin etki ettiği zaman aralığının ürünüdür. Matematiksel olarak, dürtü I = FΔt şeklinde yazılabilir, burada I ns cinsinden dürtüdür, F newton cinsinden uygulanan kuvvettir ve Δt saniye cinsinden zaman aralığıdır.
İtme ve Momentum İlişkisi
İtme ve momentum arasındaki ilişki, itme-momentum teoremi ile açıklanır. İtme-momentum teoremi, bir nesneye etki eden bir dürtü, nesnenin momentumundaki değişime eşit olduğunu belirtir.
(Ayrıca şunu okuyun: 3 Malzeme Sınıflandırmasını Bilin)
Newton'un ikinci yasasına göre, bir nesneye uygulanan kuvvetin (F), birimin momentumundaki (Δp) zaman içindeki değişime (Δt) eşit olduğunu belirtir. Matematiksel olarak, itme ve momentumdaki değişim arasındaki ilişki şu şekilde yazılabilir: I = Δp = p2 - p
Momentum Bağışıklık Yasası
Momentum bağışıklığı yasası, sisteme etki eden herhangi bir dış kuvvet yoksa, nesnenin çarpışmadan önceki ve sonraki momentumunun aynı olduğunu belirtir. Bu, çarpışmadan önceki nesneler sisteminin toplam momentumunun her zaman çarpışmadan sonra nesneler sisteminin toplam momentumuna eşit olduğu anlamına gelir. Matematiksel olarak, momentum bağışıklığı yasası şu şekilde yazılabilir: m1v1 + m2v2 = m1v1 ′ + m2v2 ′
Bilgi:
M1, nesnenin kütlesidir
m2, 2 nesnesinin kütlesi
v1, çarpışmadan önceki nesne 1'in hızıdır
v2, 2. nesnenin çarpışmadan önceki hızıdır
v1 'çarpışmadan sonraki nesne 1'in hızıdır
v2 ', 2. nesnenin çarpışmadan sonraki hızıdır.
Çarpışma
Çarpışmalar üç türe ayrılabilir, yani mükemmel esnek çarpışmalar, kısmen esnek çarpışmalar ve tamamen dirençli olmayan çarpışmalar. Çarpışmanın türünü belirlemek için, çarpışmadan sonra ve çarpışmadan önceki iki nesnenin bağıl hızları arasındaki karşılaştırmanın negatif değeri olan geri döndürme katsayısı değerinden görülebilir. Matematiksel olarak, eski haline döndürme katsayısının değeri şu şekilde yazılabilir:
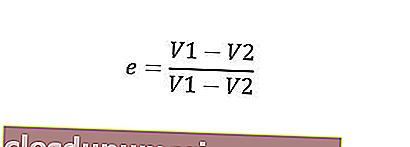
Üç tür çarpışma için geri yükleme katsayılarının değerleri şunlardır:
Mükemmel dirençli bir çarpışmada, e =
Kısmen esnek çarpışmalarda, 0 <e <
Esnek olmayan bir çarpışmada, e = 0









