Araba ve motosiklet lastikleri daireseldir, plakalar da daireseldir, şişe kapakları da daireseldir ve hatta birçok duvar saati bile dairesel şekle sahiptir. Günlük yaşamda sıklıkla karşılaştığımız bu tek düz yapı, böylece şekli tanıdık. Şimdi bu tek düz şekli, tanımı ve bir çemberin çevresi için formül hakkında öğrenmenin tam zamanı. Bunu daha iyi anlamanıza yardımcı olabilecek soru örnekleri de var. Hadi, başlayalım.
Daire, çember üzerindeki tüm noktaların merkezden aynı uzaklıkta olduğu bir şekildir. Çember üzerindeki herhangi bir nokta ile merkez arasındaki mesafeye yarıçap denir.
Bir çemberin birkaç bölümü vardır, örneğin:
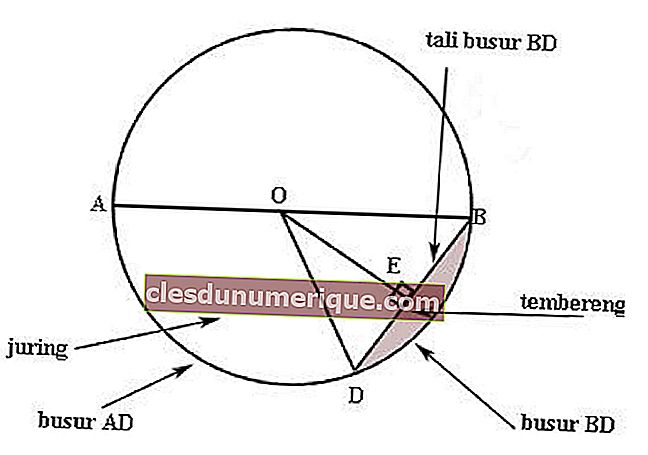
Resim kaynağı: formularumus.com
Merkez Nokta (O)
Daire üzerindeki herhangi bir nokta ile nokta arasındaki mesafenin daima sabit olduğu çemberin merkez noktasıdır.
Parmaklar
Merkez noktasını daire üzerindeki noktaya bağlayan düz bir çizgidir. Yarıçap, merkez noktası ile daire üzerindeki nokta arasındaki mesafedir.
Yay Halatı
Daireyi iki farklı noktada kesen bir daire içinde düz bir çizgi.
Ark
Daire içinde eğri bir çizgidir.
Çevre
Çemberdeki en uzun yaydır.
Çap
Merkezdeki en uzun ip, çap olarak adlandırılır. Çapın uzunluğu yarıçapın iki katıdır. Bu çap, daireyi iki eşit parçaya böler.
Apothem
Kiriş ipi ile dairenin merkezi arasındaki en kısa çizgi.
Jüring
Bir yay ve iki yarıçapla sınırlanmış bir dairenin alanı.
Potsherd
Kirişli bir yay ile sınırlanmış daire içindeki alan.
Bu parçaların dışında bir daire aşağıdaki özelliklere de sahiptir:
- Bir tarafı var
- Köşesi yok
- Bir dairenin sonsuz katlanma simetrisi vardır
- Bir çemberin sonsuz dönme simetrisi vardır
- Merkezden çember üzerindeki herhangi bir noktaya olan mesafe her zaman aynıdır
Şimdi bir çemberin çevresini hesaplamak için formülü inceleyelim.
Çevre formülü
Bir çemberin çevresi, bir çember üzerindeki bir noktadan tam bir dönüşte ve orjinal noktaya geri olan mesafedir. Bir çemberin çevresini hesaplamak aslında zor bir şey değildir. Bir çemberin çevresini hesaplamak için onu kullanmanın iki yolu vardır. Yarıçap verilirse veya çap biliniyorsa.
İkinci formül şu şekildedir:
Bilinen yarıçap:
C = 2 x π xr
Bilinen çap:
C = π xd
π = 22/7 yarıçap (r) veya çap (d) 7'nin katı ise veya 7'ye bölünebilirse kullanacağız
π = 3.14 yarıçap (r) veya çap (d) 7'nin katı değilse veya 7'ye bölünemiyorsa kullanacağız
Şimdi bu sorunun bir örneğine bakalım:
1. Bir dairenin 7 cm yarıçapı vardır. Çemberin çevresi nedir?
Çözüm:
Çevre = π x 2 x yarıçap, o zaman
K = 22/7 x 2 x 7 = 44 cm
2. 10 m çapında dairesel bir balık havuzu, balık havuzunun çevresi nedir?
Çözüm:
Çevre = π xd, o zaman
K = 3,14 x 10 = 31,4 m
Bu, bir dairenin çevresi için formül hakkında küçük bir tartışma, bununla ilgili sorularınız varsa, yorumlar sütununa yazmaktan çekinmeyin. Bunu da paylaşmayı unutma!